并查集快速上手

引言

并查集在OI竞赛中属于易掌握（不过10行）且有用（Kruskal基础）的算法之一。然而网上已经有一堆博客介绍这个算法了，质量参差不齐。

本文希望通过最直观的解释，让对本算法不熟悉的同学能在10分钟内了解算法的内容，甚至将其记忆下来。

如果下面的介绍没有对你太大的帮助，你还可以参考（以下选自百度和谷歌搜索结果第一页）：

假设我们现在有一些元素，每个元素初始时颜色不同。

现在我们把相同颜色的元素列为一个集合，就得到了很多单元素集合。

我们支持这样的操作：把一种颜色的所有元素全部变成另一种目前有的颜色

如何在几乎线性的时间内维护上述信息，使得我们可以：

就是并查集要做的事情。

（注：其实不是线性而是逆Ackermann，但由于太小所以使用时可以视为线性）

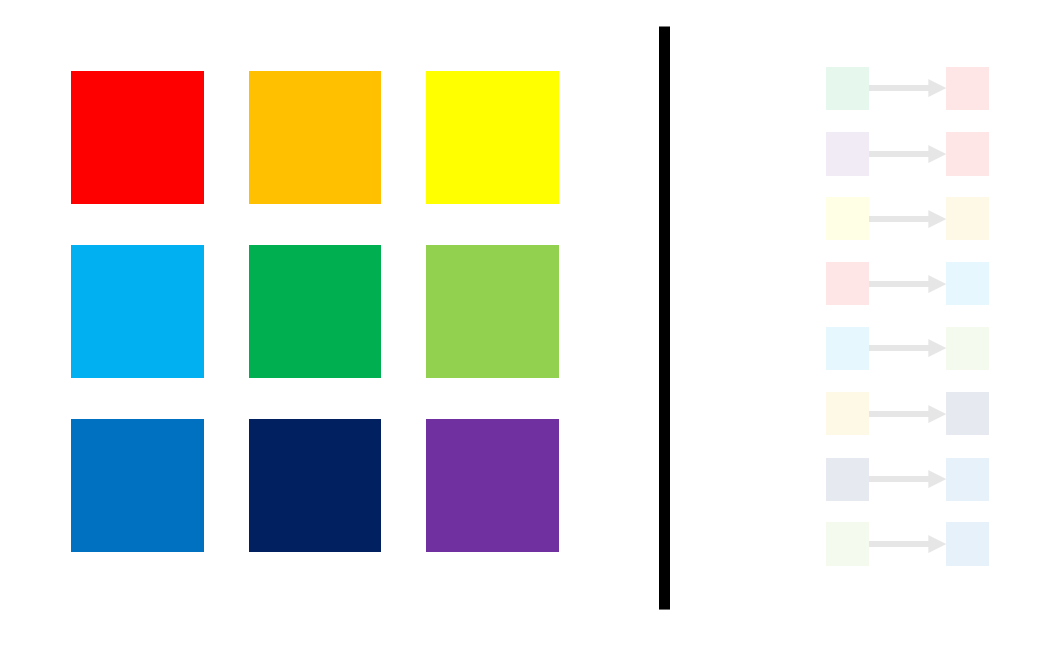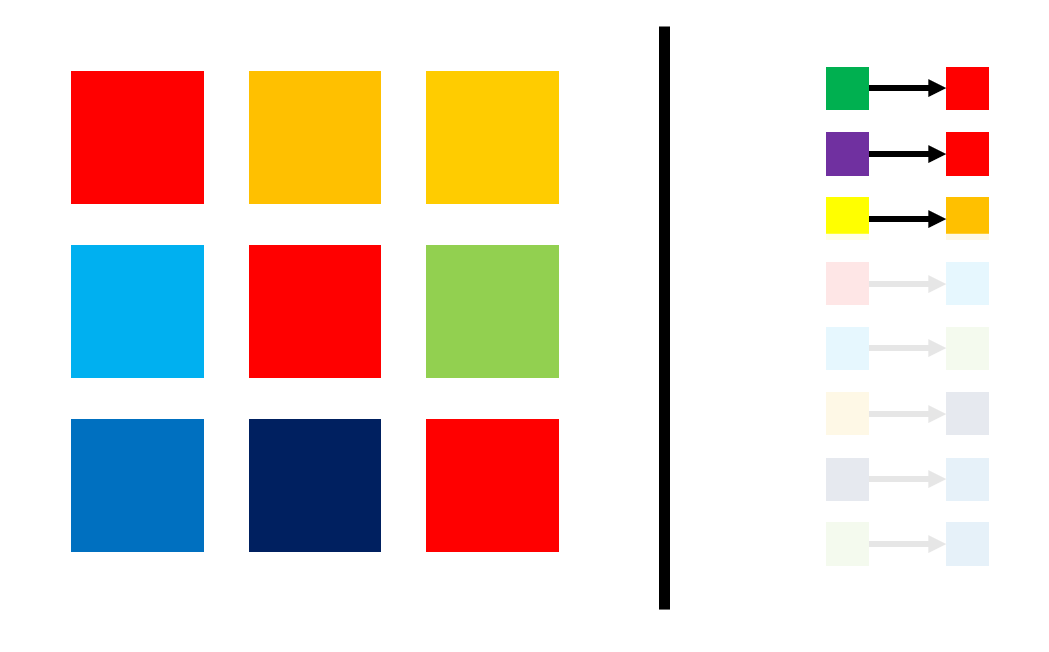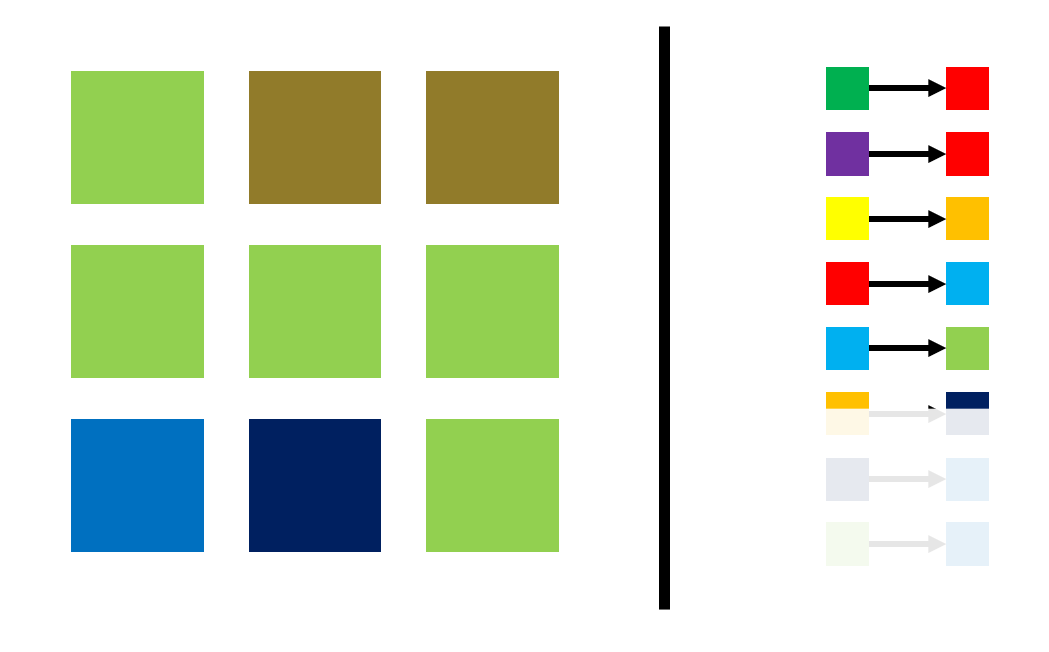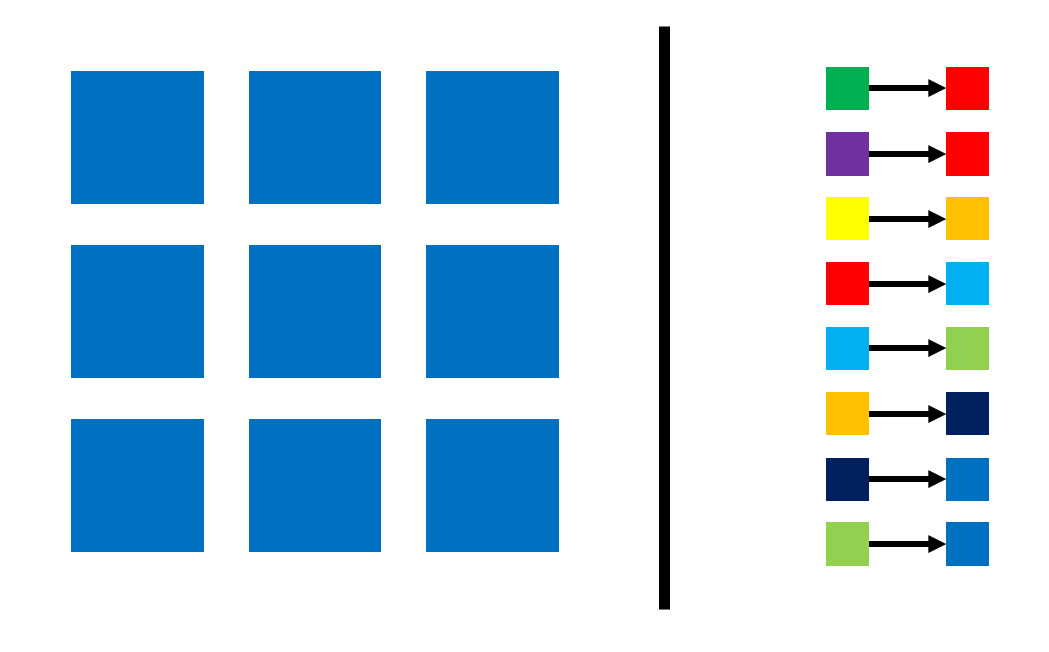
并查集-颜色合并

并查集共有两种操作：

实现的时候，我们使用一个数组记录每个元素的颜色，如果有100个元素的话：

initialize an array called color[100]

我们用标号表示颜色，不同的标号表示不同的颜色，相同的表示相同。

初始时元素颜色均不同，我们可以这样指定：

For i = 0->99 : color[i] = i

这样i号元素就会有颜色i

“查”是核心操作，通过查我们能了解一个元素的颜色。其过程是：

如果这个点的颜色还是原来的编号，说明还是原来的颜色，查完了结束。
如果这个点的编号被改成了别的，那就看看被改的那个颜色是啥，递归的查上去，并且更新其颜色。（更新颜色这一步也被称为“路径压缩”，是几乎线性的必要条件）

def find(x):
    if color[x] == x: return x
    color[x] = find(color[x])
    return color[x]

“并”是把a点的颜色改为b点的颜色。我们首先通过“查”得到a点颜色是A，b点颜色是B，之后直接把A所对应的点的颜色改为B即可。

def union(a, b):
    A = find(a)
    B = find(b)
    color[A] = B

Gif较长，请耐心观看。

并查演示

想了解为什么这样做是几乎线性的同学可以看【这里】，有对于类似路径压缩算法的十分细致的复杂度分析。

学会了并查集，我们可以：